What is Accrued Income?
(Part 1)
Previous lesson: Income: Definition and Examples
Next lesson: Accrued Income Example Part 2: Debtor Pays Off His Debt
What is accrued income?
You might have heard of this term before, but do you really know what it is?
Before we get into the meat of this lesson and a full example, let's clarify its meaning:
"Accrued" refers to something that has accumulated or has been earned and is owing.
"Accrued income" is thus income that has been earned through providing goods and services which have not yet been paid for.
In other words, you've provided some goods or services on credit, and another business owes you for that.
Be sure to check your understanding of this lesson by taking the quiz in the Test Yourself! section further below. And right at the bottom of the page, you can find more questions on the topic submitted by fellow students.
Accrued Income and Debtors
Before we go any further, let's go over another key term:
As mentioned in previous lessons, debtors are people that owe your business money.
"Debtors" also refers to the value of these debts as a whole.
Another common term used instead of debtors is accounts receivable. It means the exact same thing.
Debtors or accounts receivable is an asset, as you expect to receive benefits from them in the future – you expect to be paid.
The word "receivable" simply means "capable of being received," or "to be received."
By the way, what do you think happens if someone owes you money but you don’t expect them to pay you in the future? Well, there are no expected future benefits then, so that debt to you is not recognized as an asset.
Accrued Income Example #1
f) George’s Catering provides catering services for a funeral for the Smiths. The services are provided on the 8th of April and the agreed fee is $5,000. As part of the agreement, the Smiths will only make payment at the end of April.
George’s Catering stood as follows:
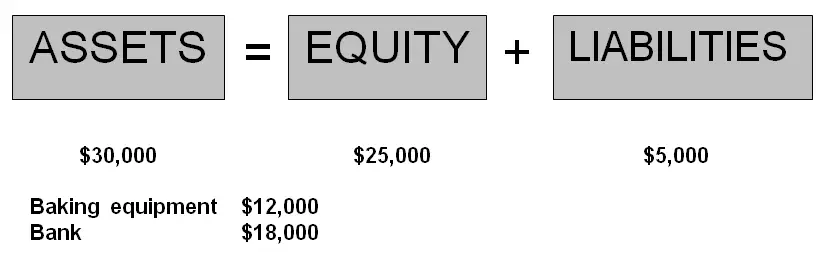
What do we do with our accounting equation on the 8th of April?
Well, before I answer that question we're going to have to look at a very key concept you need to understand - the way we record income and expenses - a concept known as the accrual basis of accounting...
The Accrual Basis of Accounting
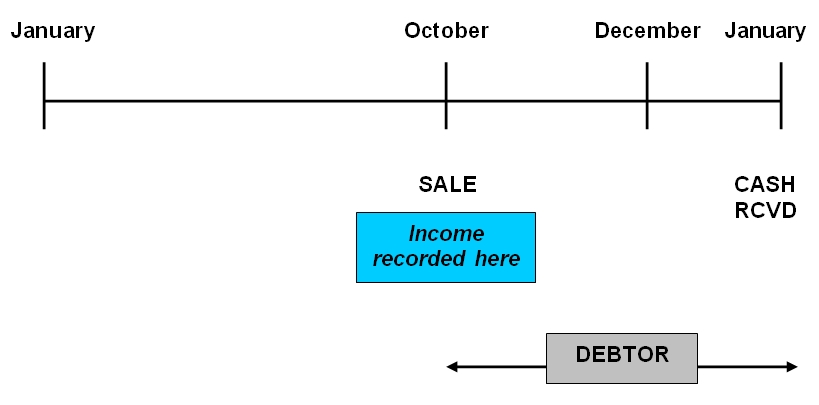
Income and expenses are recorded using the accrual basis of accounting.
The accrual basis of accounting means that if a sale is made in October, but cash is received in January, the income is recorded in October (not when the cash is received in January).
Between October and January we record that cash is owed (a debtor is recognized).
The accrual basis means that income and expenses are recorded in the periods to which they relate, and not necessarily when cash is received or paid.
In this case, cash was received the following accounting period (year) in January. In spite of this, we recognize the income this year, when it took place.
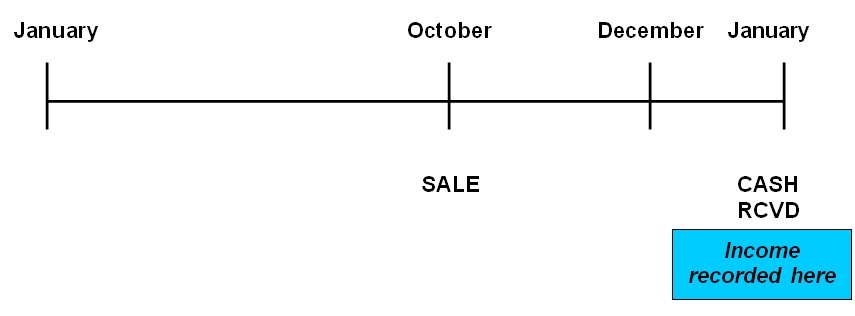
The Cash Basis of Accounting
The only other basis on which income and expenses could ever possibly be recorded is the cash basis. According to the cash basis, the income would have been recorded when the cash was finally received in January (the following year). No debtor (a credit item) would ever be recorded anywhere.
Please note: We do not use the cash basis in accounting.
We use the accrual basis.
Back to Our Accrued Income Example
So, the question still remains to be answered: what do we do with our accounting equation on the 8th of April when the catering services were provided?
Again, George’s Catering stood at:
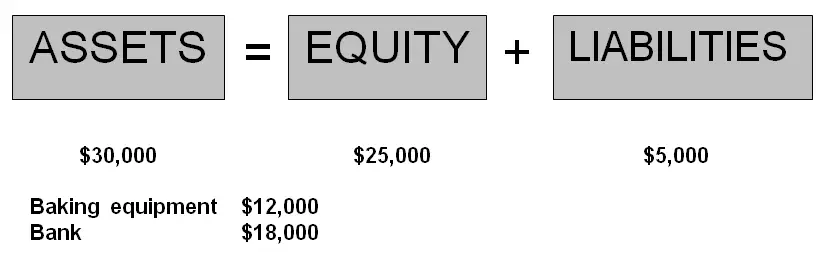
The answer is that we do the following:
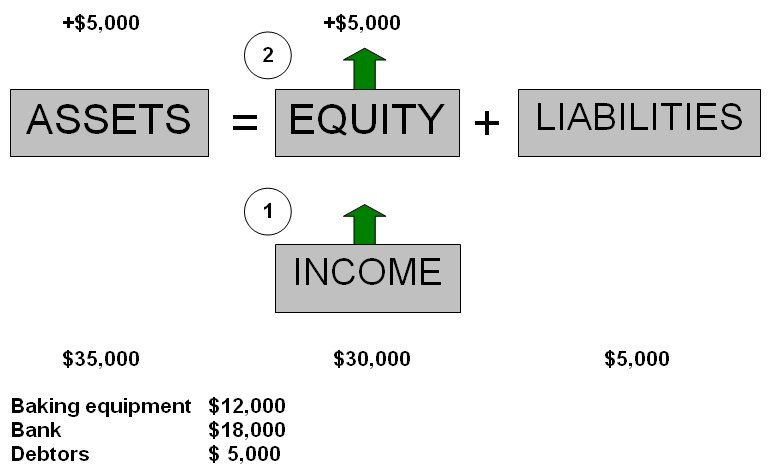
First of all, the income is recorded straight away on the 8th of April, as the event has taken place - the catering services for the funeral has been provided. The business has made income, and this is worth $5,000.
Income increases on the right side (the same side as the owner’s equity) as it belongs to the owner.
As the $5,000 is not yet received in cash, we record a debtor (the Smiths) on this date. Our assets still go up by $5,000, but this is in the form of debtors - not cash - because this was a credit transaction.
Want to see the full journal entry for this accrued income transaction?
In terms of the accounting equation and financial position of George's Catering (as shown in the diagram above), you can see that the owner now has a stake of $30,000 out of the total assets of $35,000.
So even though no cash was received yet, the income still results in more assets, and in the owner having a greater share of these assets (more owner's equity).
Test Yourself!
Before you start, I would recommend to time yourself to make sure that you not only get the questions right but are completing them at the right speed.
Difficulty Rating:
Beginner
Quiz length:
4 questions
Time limit:
6 minutes
Important: The solution sheet on the following page only shows the solutions and not whether you got each of the questions right or wrong. So before you start, get yourself a piece of paper and a pen to write down your answers. Once you're done with the quiz and writing down your answers, click the Check Your Answers button at the bottom and you'll be taken to our page of solutions.
Good luck!
Well done on completing this first tutorial on Accrued Income, hopefully you can now confidently answer the question: "What is Accrued Income?"
In our next lesson, part 2 on Accrued Income, we'll go over the second example relating to the funeral services that were provided - recording the payment from the debtor at the end of the month.
By the way, if you've been going through our lessons in order, this one is by far the most difficult so far. So if you're not feeling 100% yet, don't worry.
IMPORTANT: Do not move forward if you're confused. Instead, take a step back to the previous lesson entitled Income: Definition and Examples and go over the examples in it. When you're happy with that lesson, return to this one and check it over again. If you're still having trouble, return to earlier lessons you didn't feel good about, even the lessons in Basic Accounting Concepts. See if you can spot anything you didn't quite get the first time.
Once you're relatively comfortable with this lesson and the concept of accrued income, feel free to move ahead.
Return to Basic Accounting Transactions
Return to the Home Page
Stay up to date with ABfS!
Follow us on Facebook:
Previous lesson: Income: Definition and Examples
Next lesson: Accrued Income Example Part 2: Debtor Pays Off His Debt
© Copyright 2009-2023 Michael Celender. All Rights Reserved.
Click here for Privacy Policy.








Comments
Have your say about what you just read! Leave me a comment in the box below.